20. Первый признак равенства треугольников

Для установления равенства треугольников оказывается необя­зательно проверять равенство всех пар сторон и углов, а достаточно проверить равенство только некоторых из них. Соответствующие теоремы называются признаками равенства треугольников.

Теорема (Первый признак равенства треугольников). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Пусть АВС и A1В1C1 - два треугольника, у которых АВ = А1В1, AC.=A1C₁ A = A1 (рис. 20.1).

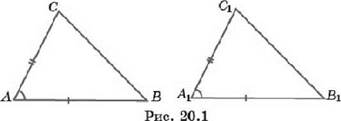
Отложим треугольник АВС от луча A1В1С1 в полуплоскости, определяемой вершиной Сь При этом вершина А совместится с вер­шиной А1. В силу равенства сторон АВ и А1В1, вершина В совместится с вершиной В\. В силу равенства углов А и А\, сторона АС пойдет по стороне AQ, и в силу равенства этих сторон, вершина С совместится с вершиной Ci. Таким образом, треугольник ЛВС совместится с треугольником А\В\С\. Следовательно, эти треугольники равны. ■

Вопросы

1.        Какие теоремы называются признаками равенства треуголь­ников?

2.        Сформулируйте первый признак равенств а треугольников.

Задачи

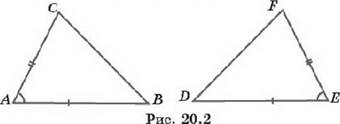
1°. Равны ли треугольники, изображённые на рисунке 20.2, если АВ = DE, АС = ЕЕ и угол А равен углу Е1

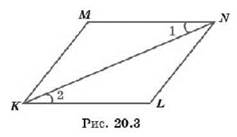
2°. Равны ли тре­угольники KLN и NMK, изо­бражённые на рисунке 20.3, если KL = NM, Z 1 =Z 2?

3.                        На рисунке 20.3 KL — NM = 4 см, угол 1 равен углу 2, КМ = 3 см. Найдите LN.

4°. Равны ли треугольники АВН и СВН, изображённые на рисунке 20.4, если В И _1_ АС и AN = СН1

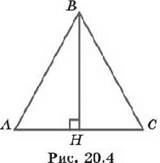
5.             На рисунке 20.4 ВН перпендикулярна АС и АН = СН = 2 см, АВ — 5 см. Найдите ВС.

Е

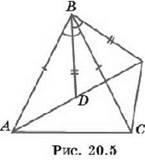
6°. На рисунке 20.5 отмечены равные отрезки и равные углы. Найдите равные треугольники.

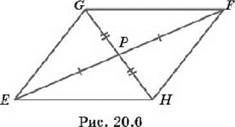
7.             На рисунке 20.6 точка Р- середина отрезков EF и GH. Есть ли на этом рисунке равные треугольники?