9. Углы

Рассмотрим два луча с общей вершиной (рис. 9.1) Они разби­вают плоскость на две части.

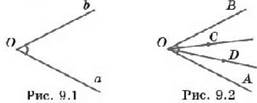
Фигура, образованная двумя лучами с общей вершиной и одной из частей плоскости, ограниченной этими лучами, называется углам. Общая вершина лучей называется вершиной угла, а сами лучи - сто­ронами угла.

Угол обозначается или одной буквой, указывающей его верши­ну, или тремя буквами, средняя из которых указывает вершину угла, а крайние- какие-нибудь точки на сторонах угла. Например, <A, <AOB и т. д. Иногда углы обозначаются цифрами, например, <1, <2 ит. д.

Точки угла, не принадлежащие его сторонам, называются внут­ренними. Лучи, исходящие из вершины данного угла и проходящие через внутренние точки угла, называются внутренними.

На рисунке 9.2 изображён угол АОВ. Точки С и D - его внут­ренние точки, лучи ОС и OD- его внутренние лучи.

Угол называется развёрнутым, если его стороны вместе со­ставляют прямую (рис. 9.3, а). В противном случае угол называется не­развёрнутым.

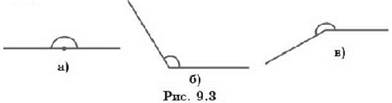
Неразвёрнутый угол может быть меньше развёрнутого, т. е. яв­ляться частью развёрнутого угла (рис. 9.3, 6), или быть больше развёр­нутого, т. е. содержать развёрнутый угол (рис. 9.3, в).

Как правило, если не оговорено противное, мы будем рассмат­ривать углы, меньшие развёрнутых.

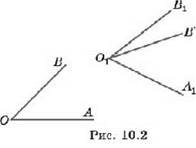
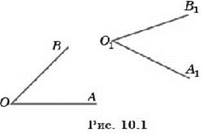
Два угла называются смежными, если одна сторона у них об­щая, а две другие составляют вместе прямую (рис. 9.4, а).

Два угла называются вертикальными, если стороны одного уг­ла дополняют до прямых стороны другого угла (рис. 9.4, 6).

Вопросы

Задачи

1.        Изобразите лучи ОА, ОB, ОС, OD так, чтобы: а) луч ОС лежал внутри угла AОВ, а луч OD лежал внутри угла ВОС\ б) луч О А лежал внутри угла ВОС, а луч ОС лежал внутри угла AOD.

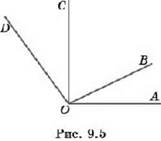
2.                    Сколько всего углов, меньших развёрнутого, определяется лучами, изображёнными на рисунке 9.5? Назо­вите их.

3.                    Сколько имеется углов, смеж­ных данному?

4.                    Сколько имеется углов, верти­кальных с данным?

6.        По рисунку 9.6 запишите пары вертикальных углов.

7.        На прямой отмечены: а) 2 точки; б) 3 точки; в) 4 точки; г)*«точек. Сколько получилось развёрнутых углов с вершинами в этих точках?

8.        На сколько частей делят плоскость: а) два луча с общей вершиной; б) три луча с общей вершиной; в) четыре луча с общей вершиной; г) « лучей с общей вершиной?