1.Вводная беседа

Геометрия - один из самых увлекательных и важных разделов математики. Зачем же она нужна?

Во-первых, именно она знакомит с разнообразием пространст­венных форм, формирует необходимые пространственные представ­ления.

Во-вторых, геометрия даёт метод научного познания, способст­вует развитию логического мышления.

Кроме этого, изучение геометрии способствует приобретению необходимых практических навыков в изображении, моделировании и конструировании пространственных фигур, в измерении основных геометрических величин (длин, углов, площадей, объёмов).

Наконец, геометрия и сама по себе очень интересна. Она имеет яркую историю, связанную с именами знаменитых учёных: Пифагора, Евклида, Архимеда, И. Кеплера, Р. Декарта, Л. Эйлера,

Н.И. Лобачевского и др.

Она возникла и развивалась в связи с потребностями практи­ческой деятельности человека. С древних времён люди сталкивались с необходимостью находить расстояния между предметами, определять размеры участков земли, ориентироваться по расположению звёзд на небе и т. п.

Слово геометрия - греческое, оно означает "землемерие” (гео - земля, метрео - измеряю).

Геометрия состоит из двух разделов: планиметрии и стерео­метрии.

Планиметрия - средневековый термин, первая часть которо­го - "плани" - происходит от латинского слова "плоскость", а вторая - ^" метрия" - от греческого "мерить", буквально планиметрия означает «плоскомерие». В планиметрии изучаются плоские фигуры, т. е. расположенные в одной плоскости.

Стереометрия - греческое слово, составленное из «стерео» - тело, и «метрео» - измеряю. Таким образом, стереометрия- это «теломерие». В стереометрии изучаются неплоские фигуры, т. е. не лежащие в одной плоскости. Чаще их называют пространственными.

О зарождении геометрии в Древнем Египте около 2000 лет до нашей эры древнегреческий учёный Геродот (V в. до н. э.) написал следующее: "Сеозоострис, египетский фараон, разделил землю, дав: каждому египтянину участок по жребию, и взимал соответствующим образом налог с каждого участка. Случалось, что Нил заливал тот или иной участок, тогда пострадавший обращался к царю, а царь посылал землемеров, чтобы установить, на сколько уменьшился участок, и со­ответствующим образом уменьшить налог. Так возникла геометрия в Египте, а оттуда перешла в Грецию".

При строительстве различных сооружений необходимо было рассчитывать, сколько материала пойдёт на постройку, вычислять расстояния между точками в пространстве и углы между прямыми и плоскостями, знать свойства простейших геометрических фигур. Так, египетские пирамиды, сооружённые за две, три и четыре тысячи лет до нашей эры, поражают точностью своих метрических соотношений, свидетельствующих, что их строители уже знали многие геометрические положения и расчёты. Одна из самых известных и больших пирамид - пирамида Хеопса (XXVIП в. до н. э.). Её высота достигает 146,5 м, а основанием служит квадрат, сторона которого равна 233 м. Это сооружение, сотворённое человеком, считалось самым высоким на Земле вплоть до XIX века.

Развитие торговли и мореплавания требовало умений ориенти­роваться во времени и пространстве: знать сроки смены времён года, уметь определять своё местонахождение по карте, измерять расстояния и находить направления движения. Наблюдения за Солнцем, Луной, звёздами и изучение законов взаимного расположения прямых и плос­костей в пространстве позволило решить эти задачи и дать начало но­вой науке - астрономии.

Начиная с VII века до нашей эры, в Древней Греции создаются так называемые философские школы, в которых происходит постепен­ный переход от практической к теоретической геометрии. Всё большее значение в этих школах приобретают рассуждения, с помощью кото­рых удавалось получать новые геометрические свойства, исходя из не­которого перечня свойств, принимаемых без доказательства и называ­емых аксиомами.

Одной из самых первых и самых известных школ была пифаго­рейская (VI-V вв. до н. э.), названная так в честь своего основателя Пифагора.

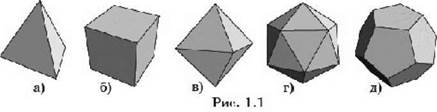
Объяснение устройства мира пифагорейцы тесно связывали с геометрией. Так, выделяя первоосновы бытия, они приписывали их атомам форму правильных многогранников, а именно: атомам огня - форму тетраэдра (рис. 1, а), земли - гексаэдра (куба, рис. 1, 6), возду­ха - октаэдра (рис. 1 в), воды - икосаэдра (рис. 1, г). Всей Вселенной приписывалась форма додекаэдра (рис. 1, д). В названиях этих много­гранников указывается число граней (от греч. эдра-грань): тетра - четыре, гекса - шесть, о кто - восемь., икос и - двадцать, додека - двена­дцать.

Более поздняя философская школа- Александрийская, инте­ресна тем, что дала миру знаменитого учёного Евклида, который жил около 300 г. до нашей эры. В одном из своих сочинений математик Папп (Ш в. н. э.) изображает его как человека исключительно честного, тихого и скромного, которому были чужды гордость и эгоизм. Насколько серьёзно и строго он относился к изучению математики, можно судить по следующему известному рассказу. Царь Птолемей спросил у Евклида, нельзя ли найти более короткий и менее утоми­тельный путь к изучению геометрии, чем его "Начала". Евклид на это ответил: "В геометрии нет царского пути".

Именно "Начала" создали славу Евклиду. В них впервые было представлено стройное аксиоматическое строение геометрии. На про­тяжении около двух тысячелетий этот труд остаётся основой изучения систематического курса геометрии.

Идея аксиоматического построения геометрии, предложенная и реализованная Евклидом, состоит в том, что если мы не можем опре­делить, что представляет собой исследуемый объект, то следует опре­делить его свойства, выделить существенные признаки объекта и аб­страгироваться от несущественных. Эти свойства называются аксио­мами, что в переводе с греческого языка означает "достойное призна­ния, не вызывающее сомнения”.

Например, фигуры шахматного слона могут быть сделаны из разных материалов, иметь разную форму, быть непохожими на насто­ящих слонов. Все эти признаки не являются для них существенными.

Существенными являются правила (аксиомы), по которым они могут передвигаться по шахматной доске.

Каждая наука имеет свои определённые правила. Б повседнев­ной жизни также приходится иметь дело с теми или иными правилами. Например, различные игры основываются на правилах. При работе с компьютером руководствуются определёнными правилами. Свод зако­нов, регулирующих деятельность человека в той или иной области, также представляет собой набор правил.

Аналогичным образом аксиомы геометрии можно рассмат­ривать как правила игры в геометрию. Используя аксиомы, путём ло­гических рассуждений, выводятся (доказываются) свойства геометри­ческих фигур, называемые теоремами. Особую роль при этом играют логические рассуждения - доказательства Несмотря на то, что неко­торые свойства геометрических фигур могут показаться вытекающими из рисунка, тем не менее, они нуждаются в доказательстве. Рисунок помогает найти доказательство, но не заменяет его.

Б последние столетия возникли и развивались новые направ­ления геометрии, среди которых: геометрия Лобачевского, топология, теория графов и др. Появились новые методы, в том числе координат­ный и векторный, позволяющие переводить геометрические задачи на язык алгебры и наоборот. Геометрия широко используется в других науках: физике, химии, биологии, экономике и др.

Вопросы