Уроки 1-2. Элементарные построения

Задачей уроков является отработка навыков построения циркулем и линейкой и в программе «Живая геометрия».

Необходимые знания: теоремы о признаках равенства треугольников, признаках и свойствах параллелограмма, признаках и свойствах параллельности прямых, движения, расстояние от точки до прямой,

Вводная часть: рассказ об истории вопроса, построения циркулем и линейкой в древней Греции.

Описываем порядок действий при решении задач на построение: анализ,

построение, множество решений, доказательство.

1.Построение треугольника по трем сторонам.         

-Анализ: при помощи линейки можно провести луч АВ, при помощи циркуля – построить на нем отрезок заданной длины.

Вершина С находится на пересечении множеств точек, удаленных на расстояние АС от точки А (окружности с центром в точке А и радиусом АС), и множества точек, удаленных на расстояние ВС от точки В ( окружность с центром в точке В радиусом ВС).

3.Строим окружность с центром в точке А радиусом АС.

4.Строим окружность с центром в точке В радиусом ВС.

5. Точка пересечения окружностей является третьей вершиной треугольника.

Построение в "Живой геометрии":

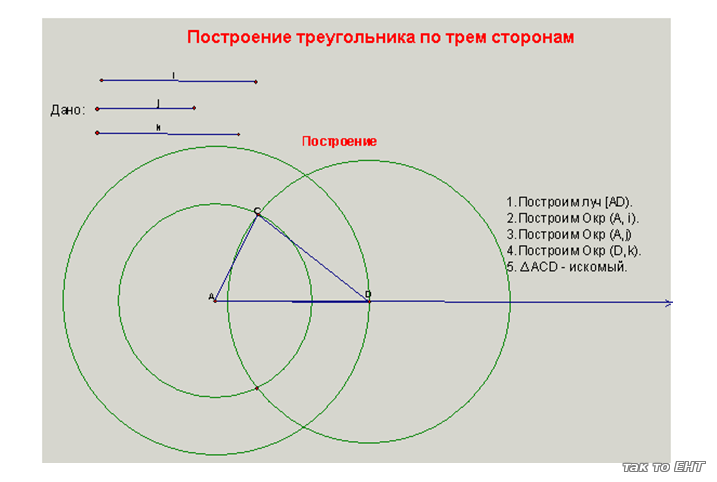
-Множество решений: задача имеет два решения;

в «Живой геометрии» есть возможность показать при каких значениях длин отрезков задача имеет решение (неравенство треугольника).

-Доказательство: полученный треугольник согласно построению удовлетворяет условию задачи.

2.Построение угла, равного данному.

-Анализ: сводим задачу к построению равного треугольника циркулем и линейкой и к повороту в построении в «Живой геометрии».

-Построение циркулем и линейкой:

Проводим окружность с центром в вершине заданного угла, точки пересечения окружности со сторонами угла и вершина угла образуют треугольник, одним из углов которого является заданный угол.

-Построение в «Живой геометрии»

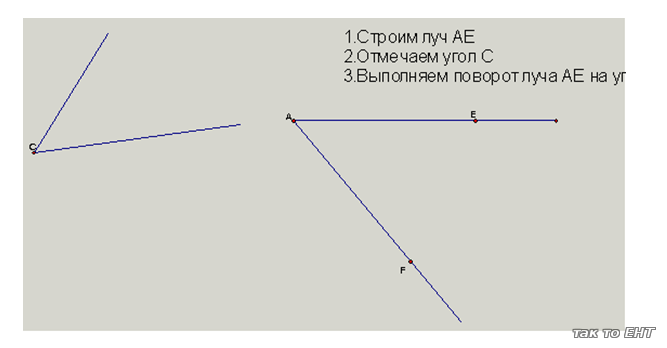
-Множество решений: задача имеет два решения.

-Доказательство: угол Е равен углу С согласно построению.

3.Построение треугольника по двум сторонам и углу между ними.

-Анализ: задача сводится к построению угла, равного данному.

-Построение циркулем и линейки:

            1.Строим угол, равный данному.

2.На сторонах угла откладываем длины заданных отрезков.

3.Соединяем полученные точки отрезком.

-Построение в программе «Живая геометрия»

-Множество решений: задача имеет четыре решения.

-Доказательство: треугольник DEF является искомым, так как содержит заданный угол и две стороны с заданными длинами.

4.Построение треугольника по стороне и двум прилежащим к ней углам.

            Самостоятельная работа.