Урок №47. Тема: Теоремы о перпендикулярности диаметра и хорды.
Цель:
- обеспечение
прочности знаний и совершенствование способов деятельности при нахождении
элементов окружности, и величины центрального угла, формировать умение
использовать теоремы при решении задач.;
- развитие
вычислительных навыков, развитие логико-структурного мышления; формирование
навыков нахождения рациональных путей решения и достижения конечных
результатов; развитие познавательной деятельности и творческого мышления.
– формирование у учащихся ответственности,
системности; развитие познавательных и эстетических качеств; формирование информационной культуры учащихся.
Тип урока:
совершенствование знаний и способов деятельности
Вид урока: смешанный урок.
Метод обучения: практический.
Форма обучения: коллективная.
Средства обучения:
доска, мел
ХОД УРОКА:
I.
Организационный этап (2 мин).
Образовательные задачи:
- обеспечение нормальной внешней
обстановки для работы на уроке;
- психологически настроить учащихся к общению
Содержание этапа;
- приветствие;
- проверка подготовленности к уроку;
- постановка целей урока и плана проведения
II.
Актуализация субъектного опыта учащихся (5 мин).
Образовательные задачи:
- обеспечение мотивации учения
школьников;
- актуализация субъектного
опыта.
Содержание этапа;
- выяснение степени усвоения учащимися заданного учебного материала;
- выявление знаний об окружности и её элементах
Ребята! Давайте
вспомним:
1) Что такое окружность?
2) Что является элементами окружности?
3) Что такое радиус окружности?
4) Что такое хорда?
5) Что такое диаметр окружности?
6) Какой угол
называется центральным?
7) Что называют
геометрическим местом точек?
8) Чему равна градусная мера полной окружности?
9) Что такое дуга?
10) Чему равна градусная величина дуги?
III. Проверка домашнего задания (10 мин)
§1, № 224,226 стр67
IV. Формирование умений и навыков (20 мин)
Теорема 1:Диаметр окружности,
проходящий через середину хорды, перпендикулярен ей.
Доказательство: Пусть точка С – середина
хорды АВ и
прямая ОС пересекает
окружность в точках Е и F.
Покажем, чтоTF АВ.
АВО равнобедренный, так, как АО и ОВ –
радиусы
окружности, ОС – его
медиама. Тогда по свойству медианы
равнобедренного
треугольника ОС является и высотой
треугольника АОВ, т.е. ОС АВ. Следовательно,EF
AВ.
V.Применение.
Формирование умений и навыков
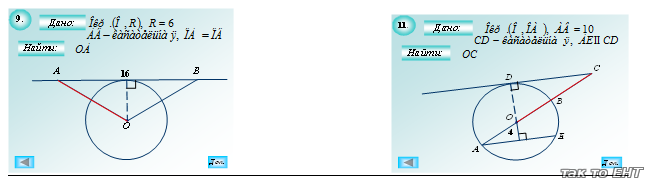
Решение задач из учебника.
№№ 209,210211 стр 66
V. Домашнее задание(2 мин.)
§1, №
215,216 стр66
VI. Подведение итогов урока (3
мин.)
( дать качественную оценку
работы класса и отдельных учащихся).
VII. Этап рефлексии (2 мин.)
|
|

Будь-те первым, поделитесь мнением с остальными.
