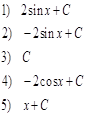Разноуровневые задания по алгебре 10 11 классы

  Задания   составлены  в соответствии с программой по математике вобщеобразовательной школе (направление: естественно-математическое),  позволяютопределить уровень знаний, умений, отработать пробелы, тем самым качественноподготовиться к сдаче экзаменов.

Отличительнаяособенность работы в том, что материал представлен  согласно технологииуровневой дифференциации, содержит задания трех уровней.

 

    

Тема:  Применение производной.       Уровень  А.   1.   Исследуйте функцию на экстремум:   f(x)= -x²+ 7x
1)   x=3,5,  точка максимума
2)   х=1,  точка минимума
3)   х=3,5 ,  точка минимума
4)   х=7,  точка максимума
5)   х=0,  точка минимума

2.Исследуйтефункцию на экстремум: f(x) = x2 + 2x – 3

      A)x = 1, точкамаксимума

      B) х = -4, точкаминимума

      C) х = -1, точкаминимума

      D) х = 4, точкаминимума

      E) х = -1, точкамаксимума

3. Найтикритические точки функции у = х2 – 3х + 2

      A) 0,5

      B) 2

      C) 1

      D) 0

 

                                                                                              

Уровень  В.   1.  Пусть производная функции  f(X) имеет вид
найти суммарную длину промежутков возрастания  функции f(X).
1)  3
2)  5
3)  2
4)  4
5)  6

2.Найдите точкиэкстремумов функции и определите их вид:

у =

      A) х = 3 точка max; x = -3 точка min

      B)x = -3 точка max; x = 3 точка min

      C)x = - точка max; x =  точка min

      D)x =  точка max; x = - точка min

УровеньС.

1.Для функции Y = , определите:

      а) нули;

      б)промежутки возрастания;

      в)промежутки убывания;

 

      A) а) -3; 3;                б) нет;             в) (-;)

      B)a) -3; 3;      б)(-; 0];       в) [0; )

      C)a) 3; -3;                б) [1; 3], [-3; 0];  в) (0; -3], [0; 3]

      D)a) -3; 3;                б) нет;             в) (-; 0), (0; )

      E)a) -3; 0; 3;    б) [-3; 0], [3; );в) (-; -3], [0; 3]

 

                                                            

Тема:Первообразная.  Интеграл.       Уровень  А.                                           1.Вычислите  интеграл
2.Найдите  первообразную функции f(x) = 3e3x         A)  27e3x + C         B)         C) e3x  + C         D)         E) 9e3x  + C
3.  Найдите    первообразную  функции

 

Уровень В.

1.Найдите общийвид первообразных F(x) для функции f(x) =  на промежутке (0,5; +)

      A) F(x)=

      B) F(x)=

      C) F(x)=

      D) F(x)=

      E)F(x) =

2.Вычислитеплощадь фигуры, ограниченной графиком функции у = х(4 – х) и осью абсцисс

      A)       B)

      C)    D) 2

      E)

3.Вычислитеплощадь фигуры, ограниченной прямыми у = 4 – х, у = 3х и осью Ох

      A) 3

      B) 4

      C) 5

      D) 6

      E) 7

 

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                      

Уровень  С.       1.       Найти  общий вид первообразной для функции f(х)=sin4х.   А)  3х\8 –sin2х  +sin4х + с                    4          32

В) 3х –sin2х  +sin4х                 С) 3х –sin3х  +sinх

Д)3sin2х+sin4х                 Е) 3хsin2х+sin4х        2. Ф(х)=│3х+5│ является первообразной для ф(х)=-3 на промежутке   А)  (-5;-1)   В)  (-2;7)   С)(-5;-2)   Д)  (-3;1)   Е)(10;4).