УРОК № 50 ДЕЛЕНИЕ С ОСТАТКОМ (П. 13)

Цели: объяснить учащимся, что деление натурального числа на другое нацело не всегда возможно; научить называть компоненты при делении с остатком и выполнять деление.

Оборудование: пленка для устных упражнений; кодоскоп.

Ход урока

I. Устные упражнения.

1. № 540 (а, б, в), 541 (а, б) – просвечивается на экран.

2. Учащиеся из своего домашнего задания задают анаграммы классу.

II. Изучение нового материала.

1. Ученики читают каждый абзац пункта, обсуждают и озаглавливают, в результате получается примерно такой конспект:

а) Деление одного натурального числа на другое нацело не всегда возможно;

б) При делении с остатком числа называются так.

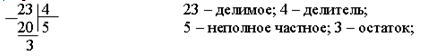
в) Остаток всегда меньше делителя;

г) Чтобы найти делимое при делении с остатком, надо умножить неполное частное на делитель и к полученному произведению прибавить остаток.

23 = 4 × 5 + 3.

III. Закрепление.

1. Ответить на вопросы п. 13.

2. № 533 (д, б, в), 533 (а, е), 532 (3-я строка); 538.

3. На повторение. № 548 (3, 4) – самостоятельно.

IV. Итог урока.

Тест

1) При делении числа на 46 может получиться остаток:

а) 48;                 б) 45;              в) 46;              г) 47.

2) Скорость пешехода 5 км/ч, а скорость велосипедиста 20 км/ч. Во сколько раз скорость велосипедиста больше скорости пешехода?

а) в 2 раза;        б) в 3 раза;     в) в 4 раза;     г) на 15 км/ч.

3) За 3 часа теплоход проплыл 105 км, а поезд за 2 часа проехал 110 км. Во сколько раз скорость поезда больше скорости теплохода?

а) в 4 раза;                    б) в 3 раза;                 в) в 2 раза.

V. Домашнее задание: п. 13 (уметь пересказать конспект); № 550 (а, в); 552; 553 (а); 555 (а, г), повторить п. 12.