Урок математики на тему: " Сравнение чисел при помощи числовой прямой"
М АОУ «»средняя общеобразовательная школа № 109» г.
Пермь
Урок математики во 2 классе.
Программа Эльконина –
Давыдова.
Тема: Сравнение чисел при
помощи числовой прямой.
Цель:
·
Организация деятельности детей по открытию
способа построения числового луча,
·
формирование навыка практической
деятельности при сравнении чисел с помощью числового луча;
·
умение находить место абстрактного числа
на числовой прямой и сравнивать их;
·
Развитие умения мыслить абстрактно,
развитие логического мышления.
Ход урока.
1. Организационный момент.
2.
- Я зашла в соседний класс перед уроком, после
математики на доске остался такой рисунок:
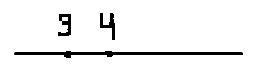
- Как вы думаете, что это было?
- Как преобразовать данный рисунок в
числовую прямую?
- Кто может это сделать на доске?
- Обозначь единичную мерку. Разметь
числовую прямую до конца, числа писать не надо.
Вывод: У нас был рисунок, и мы превратили его в числовую
прямую. Вспомните правила
построения числовой прямой.
ü НАПРАВЛЕНИЕ
ü ЕДИНИЧНАЯ МЕРКА
ü НОЛЬ
ü ВСЕ ЧИСЛА
РАСПОЛОЖЕНЫ ПО ПОРЯДКУ
- Молодцы, все назвали.
- Проверьте, все правильно? Отметьте
числа 5, 7, 2, 8, 10.
-
Итак, мы знаем как построить числовую прямую, знаем, что для этого
нужно, умеем находить числа по
числовой прямой. А для чего нам нужна числовая прямая?
- Сравните: 5 и 7,
выразите 5 через 7. 5 = ……
а 7 через 5 ? 7 = ……
а
….. а + 1
а ….. в
- Почему не можем сравнить?
- Чем сегодня будем заниматься на
уроке?
Тема:
Сегодня к концу урока мы должны
установить некоторые закономерности, правила, по которым можно сравнивать любые
числа и даже те, у которых мы не знаем их конкретного значения, например а и в.
3.
Посмотрите
на доску. Дети отметили на числовой прямой числа а, в и с и числа
а-2,
в-3, с+2. Вот
только сами числа а, в, с случайно
стерли. Покажите на числовой прямой, где находятся эти числа. Это задание вы
будете выполнять в группе.

Проверка. (повесить на доску на магниты,
по одному человеку от группы выходят и объясняют про 1 точку.)
- Почему именно здесь находится точка?
Как смогли определить, что точка … именно здесь?
Вывод: Какое правило
помогло искать числа на числовой прямой?
Физминутка. Поиграем в игру «Больше-меньше» по таблице.
Если я называю большее число- руки верх, если меньшее – руки вниз.
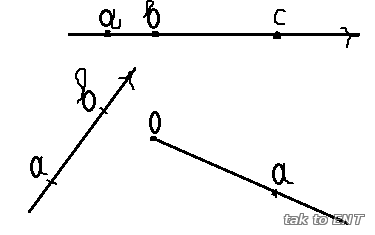
- Почему ловушка? Как догадались, что а меньше в ?
4.
Закрепление.
- Эта работа поможет вам выполнить следующее задание. Рассмотрите выражения. Как думаете, какое
задание можно выполнить?
Хорошо, сравните выражения, запишите в тетрадь.
в
– 1 … в
а
+ 2 … а
с
– 2 … с
d + 3 … d
Проверка. Чтение по
одному выражению. – А можете сказать, на сколько…
- У кого нет
ошибок, поднимите руку. Поставьте оценку.
- С этим заданием
вы справились. Смогли найти место точек а,
в, с, смогли сравнить. А теперь, пользуясь числовой прямой, попробуйте
выразить через числа через с. Вспомните,
как мы это делали с числами, а теперь покажите это в общем виде. Начало записи
даю я. Обсудите это в группе.
Проверка. Пишу на доске.
5.
–Как
думаете, а можно сравнивать без числовой прямой? Сравните в группе числа:
а … а + 3 ( на …
)
в – 2 … в ( на … )
а – 1 … а + 1 (
на …)
d – 3 … b (на …)
с – 2 … с + 3
(на …)
Проверка: Каждая группа
читает по одному выражению и комментирует.
Итог урока. У нас есть 2
числа. Всегда ли мы можем их сравнивать? Какие правила мы используем для
сравнения?
Домашнее
задание. В
одной сказочной стране у человечков были свои сказочные числа. Они отмечены на
числовой прямой. Вставьте вместо Х пропущенные сказочные числа, а вместо точек
пропущенные знаки и сравни их.
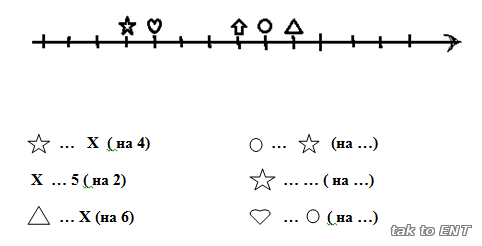

Будь-те первым, поделитесь мнением с остальными.
