10 сынып Кері тригонометриялық теңдеу, теңсіздіктер

10 сынып

Сабақтың тақырыбы:
Кері тригонометриялық теңдеу, теңсіздіктер

 

Сабақтың мақсаты: 

1. Дидактикалық:
кері тригонометриялық теңдеу, теңсіздіктерді шеше білуге
үйрету

2. Тәрбиелік:
ұқыптылыққа, жинақылыққа,
тапқырлыққа тәрбиелеу;

3. Дамытушы:
оқушының логикалық ойлауын  танымның индукция-дедукция,
қарапайым-күрделі, салыстыру-сәйкестендіру аңдары
негізінде дамыту.

Сабақтың түрі:
практикалық.

Сабақты оқыту әдісі:
ұжымдық, даралап оқыту.

Пәнішілік байланыс:
оқушылардың білімін пәнішілік интеграциялау арқылы
тиянақтау, негізгі меже – функция қасиеттерін қолдануға
бағыттау.

1. Кіріспе мотивациялық
   бөлім

1.1. Проблемалық ахуал: кері
тригонометриялық теңдеу, теңсіздіктерді шешудің дайын
формуласы жоқ болғандықтан, оны формальды операциялар
арқылы шешу мүмкін емес.

 1.2. Сабақтың міндеті: осы
проблемалық ахуалдан шығу жолдарын іздестіру: кері
тригонометриялық функциялардың қасиеттерін қолдану
арқылы қарапайым теңдеу, теңсіздіктерге көшу
жолдарын меңгеру.

1.3. Бағытталған негіздегі іс-
әрекеттер: теориялық материалды қайталап, есеп
шығарудың негізін қалау.

1.4. Өткен тақырыптың
өзектілігі: кері тригонометриялық функциялардың
қасиеттерін білу оқушыларды есеп шығару әрекетіне
дайындайды.

2. Танымдық жұмыстар

2.1. Оқушыларды қажетті ақпаратпен
қамтамасыз ету: оқу материалдарын алдын ала үлестіру.

2.2. Қосымша әдебиет қолдану:

1) Н.Я.Виленкин и др. Алгебра и начало анализа 10, 
Просвещение 2004

2) М.Л.Галицкий и др. Углубленное изучение курса
алгебры и математического анализа Москва Просвещение 1990

2.3. Деңгейлік есептер шығару

3. Бақылау, бағалау: өздік
жұмыс есептерін шығару.

4. Үйге тапсырма беру: Тарату
материалындағы есептерді шығару.

5. Сабақты қорытындылау.

 

Оқу материалының
мазмұны:

Теңдеу,
теңсіздіктерді шешкенде кері тригонометриялық функциялардың
ерекше қасиеттерін есте сақтап, олардың орындалуын
қадағалау керек.

1. 
.

 немесе .

 немесе . ,
тақ функция, өспелі функция.

2.  
.

 немесе .

 немесе . .  кемімелі
функция.

3.  
.

 ,
яғни .

,
яғни . ,
тақ функция, өспелі функция.

4.  
.

, яғни
.

,
яғни . .  кемімелі
функция.

5.  

1. 
Алдымен қарапайым теңдеу, теңсіздіктерді
қарастырайық.

1)  ,
бұл екі бұрыштың теңдігі. Теңдіктің екі
жағын синустаймыз:

.
Жауабы: .

2)  
,   болғандықтан,
.

3)  

.
Жауабы: .

4) 

,

Жауабы: .

5)  
, өспелі
функция.

 

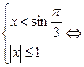
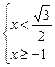
Жауабы: .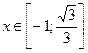

6)  

 теңдігін
пайдаланамыз:

,  .

Жауабы: .

7)  
,   болғандықтан.

Жауабы :.

8)  
,  болғандықтан,
.

Жауабы:

9) 

.

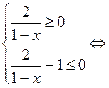
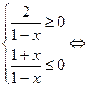
Жауабы:

10)

 қасиетін
қолданамыз.

.

Жауабы: .

11)

,
келтіру формуласын қолданамыз.

,

, .

Жауабы: .

Жаттығу

Теңдеуді
шеш:

1.           2.           3.           4.           5.           6.

7.           8.           9.           10.       11.    12.