8 сынып. Алгебра.
Квадрат теңдеулер шешудің әр түрлі тәсілдері
Сабақтың мақсаты:
а) Білімділік мақсаты:
Виет теоремасын , квадрат теңдеудің түбірлерінің формуласын пайдаланып квадрат теңдеуді шешу , қысқаша көбейту теңбе-теңдіктерін пайдаланып рационал теңдеулер шешу және теңдеу құру тақырыбынан алған білімдерін жүйелеу , логикалық есептер шығару .
ә) Дамытушылық мақсаты:
Оқушылардың өз бетімен жұмыс істеуін , ойлау қабілетін дамыту , іздендіруді жүзеге асыру
б) Тәрбиелік мақсаты:
Тәуелсіздік алғанымызға 20 жыл толуымен сабақты байланыстыра отырып, еліміздің қысқаша тарихымен таныстыру, Отанды сүюге, ана-тілін сүюге тәрбиелеу, еңбекке , тапқырлыққа , шапшаңдыққа үйрету.
Сабақтың көрнекілігі :
1. квадрат теңдеу тақырыбына байланысты формулалар .
2. Деңгейлік тапсырмалар.
3.Лото ойыны (сурет сыртында 1991х2 -2011х+20=0 деп көрнекі етіп жазылады).
4. Интерактивті тақта.
5. Магнитофон.
Сабақтың әдісі:
1. Сұрақ-жауап
2. Кітаппен жұмыс
3. Проблемалық ситуация
4. Саралап деңгейлеп оқыту
5.Дарынмен жұмыс
Пәнаралық байланыс: тарихпен, әдебиетпен, өмірмен.
Сабақтың барысы:
Сабақ мынадай сатылардан өтеді.
1.Өзектену (қызықтыру, ынталандыру, назарын аудару)
2. Қабылдау, еске алу (үй тапсырмасын сұрау)
3.Ұғыну
4.Қолдану, пайдалану (бекіту, қорыту, бағалау)
5. Игеру (үйге тапсырма беру)
1. Ұйымдастыру бөлімі.
2. І тірек сұрақтары
Квадрат теңдеудің анықтамасы.
_________________________________________________________________________
Квадрат теңдеу түбірлерінің формуласы.
________________________________________________________________________
Квадрат теңдеудің қанша түбірі болуы мүмкін?
________________________________________________________________________
Виет теоремасы
________________________________________________________________________
Толымсыз квадрат теңдеу деген не?
________________________________________________________________________
ІІ а) х1=2 х2=4 түбірлері болса, квадрат теңдеу құр.
Жауабы: х2-6х+8=0
ә) х2-8х+8=0 теңдеуінің түбірлерін іріктеп алу тәсілімен тап.
Жауабы: х1=10 х2=-2
б) х2-8х-20=0 теңдеуінің түбірлерінің көбейтіндісін және қосындысын тап.
Жауабы: х1·х2=-20
х1+х2=8
ІІІ. Лото ойыны
Үш топқа тапсырма беріледі.
Әр тапсырманың жауаптарының сыртында 1991х2-2011х+20=0 деп жазулы тұрады.
Осы есептердің жауаптары
Осы теңдеуді шешу тапсырылады.
1991х2-2011х+20=0
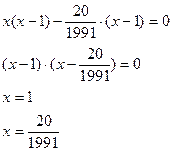
Сонымен 1991+(-2011)+20=0
Коэффициенттердің қосындысы нөлге тең болса, бір түбірі 1-ге тең болады,екінші түбірі Виет теоремасы арқылы табылады.
Осы квадрат теңдеудің коэффициенттеріне назар аударалық 1991; 2011; 20
2011жыл-
Еліміздің тәуелсіздік алғанына 20жыл толғалы отыр.
1991жыл 25 қазан – Қазақстан Республикасы егемендік алып, тәуелсіз ел болып жарияланған күн. Тәуелсіздік бізге оңайлықпен келген жоқ. Тәуелсіздіктің әр сағаты жылмен тең. Қазақ елін әлем таныды. Мың өліп, мың тірілген қазақ бабаларымыз ғасырлар бойы аңсаған тәуелсіздікке ие болды. Ал қол жеткен табыстарымыз елбасы Н.Ә.Назарбаевқа тікелей байланысты. Сондықтан біз болашақ ұрпақ Н.Ә.Назарбаев еңбегінің бағасын ерекше ризашылықпен құрметтеп қорғауымыз керек.
Ұлы Абай атамыз айтқандай «Сен де бір кірпіш дүниеге, кетігін тап та бар қалан» деп елімізді өркендетуге өз үлесімізді қосайық.
Сонымен, квадрат теңдеу шешу үшін оның коэффициенттерінің қасиеттеріне сүйеніп , оңай тәсілмен шешуге болады екен.
1. Егер а+в+с =0 ðх1=1 x2=
Дәлелдеуі.
Барлық мүшелерін а-ға бөлеміз
Виет теоремасы бойынша
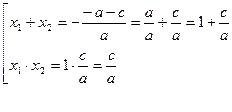
2. Егер а-в+с=0 ð
Шарт бойынша а-в+с=0
в=а+с
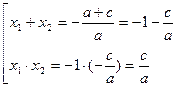
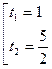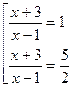ð ð ð ð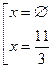
Мысал 4.
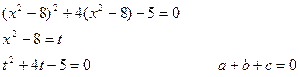
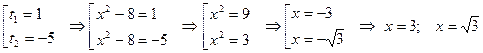
x1=60км/сағ x2=-90км/сағ (қанағаттандырмайды)
І v1=90 км/сағ
II v2=60 км/сағ
ІІ
ІІІ
х-тің қандай мәнінде х2-11х+31 үшмүшесінің мәні 1-ге тең болады.
Үйге тапсырма №213, 201 (4,5,6) 202
Оқушылар алған ұпайлары бойынша бағаланады.
Комментариев пока нет. Станьте первым, кто оставит своё мнение!
Чтобы оставить комментарий, пожалуйста, войдите на сайт.