Урок №50. Тема: Взаимное расположение двух окружностей. | Поурочные планы по геометрии 7 класс

Цель:

Образовательная - усвоение новых знаний о взаимном расположении прямой и окружности и о взаимном расположении двух окружностей;

Развивающая - развитие вычислительных навыков, развитие логико-структурного мышления; формирование навыков нахождения рациональных путей решения и достижения конечных результатов; развитие познавательной деятельности и творческого мышления.

Воспитательная – формирование у учащихся ответственности, системности; развитие познавательных и эстетических качеств; формирование информационной культуры учащихся.

Тип урока: изучение нового учебного материала.

Вид урока: смешанный урок.

Метод обучения: словесный, наглядный, практический.

Форма обучения: коллективная.

Средства обучения: доска

ХОД УРОКА:

Организационный этап (2 мин).

Образовательные задачи:

- обеспечение нормальной внешней обстановки для работы на уроке;

- психологически настроить учащихся к общению

Содержание этапа;

- приветствие;

- проверка подготовленности к уроку;

- постановка целей урока и плана проведения.

Актуализация субъектного опыта учащихся (5 мин).

Образовательные задачи:

- обеспечение мотивации учения школьников;

- актуализация субъектного опыта.

Содержание этапа;

- выяснение степени усвоения учащимися заданного учебного материала;

- выявление знаний об окружности и её элементах.

Вопросы:

1) Что такое окружность?

2) Назовите элементы окружности?

3) Что такое перпендикуляр?

Формирование умений и навыков (20 мин)

Рассмотрим, как могут располагаться между собой две окружности.

I. Взаимное расположение двух окружностей. (R₁ и R₂ – радиусы окружностей)

Случай 1.

Окружности не имеют общих точек (не пересекаются).

Если R₁ + R₂ < d,

d – Расстояние между центрами окружностей.

Концентрические окружности имеют общий центр

Случай 2:

Окружности имеют одну общую точку (касаются).

Если R₁ + R₂ = d,

Внешнее касание

Внутреннее касание

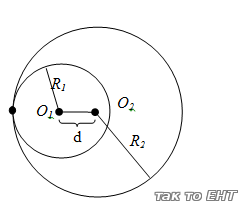
Случай 3:

Окружности имеют две общие точки (пересекаются).

Если R₁ + R₂ > d,

1) Какие случаи расположения прямой и окружности вам известны?

2) Какая прямая называется касательной?

3) Какая прямая называется секущей?

4) Теорема о диаметре, перпендикулярном хорде?

5) Как проходит касательная по отношению к радиусу окружности?

6) Как могут располагаться две окружности?

7) В каком случае окружности имеют одну общую точку?

8) Как называется общая точка двух окружностей?

9) Какие касания вам известны?

10) Когда окружности пересекаются?

11) Какие окружности называются концентрическими?

Закрепление новых знаний и способов деятельности

Решение задач из учебника.

№№ 210, 211, 212 стр66

Домашнее задание(2 мин.)

§ 1п.1.1, (выучить), № 221,222 стр67

Подведение итогов урока (3 мин.)

( дать качественную оценку работы класса и отдельных учащихся).

Этап рефлексии (2 мин.)

(инициировать рефлексию учащихся по поводу своего эмоционального состояния, своей деятельности, взаимодействия с учителем и одноклассниками с помощью рисунков)